EdgeBERT：極限壓縮，比ALBERT再輕13倍！樹莓派上跑BERT的日子要來了？ - 知乎

語言: CN / TW / HK

時間 2021-01-07 10:01:54 osc_pberzs5e

主題: adaptive 自然語言處理機器學習深度學習 lottery 物聯網 bert 反向傳播 hypothesis raspberry pi

Linux基金會Kubernetes安全專家認證上線，預約享早鳥折扣，最後三天！>>>

文 | Sheryc_王蘇
本文首發於NLP寶藏公號 【夕小瑤的賣萌屋】，瘋狂暗示！

這個世界上有兩種極具難度的工程：第一種是把很平常的東西做到最大，例如把語言模型擴大成能夠寫詩寫文寫程式碼的GPT-3；而另一種恰恰相反，是把很平常的東西做到最小。對於NLPer來說，這種“小工程”最迫在眉睫的施展物件非BERT莫屬。

從18年那個109M引數的BERT，到52M引數的蒸餾後的DistilBERT，再到14.5M引數的蒸餾更多層的TinyBERT，最後到12M引數的層級共享的ALBERT，曾經那個在叢集上載入引數都費勁的BERT現在甚至已經可以跑在手機平臺上了。當我們為BERT的輕量化歡呼雀躍之時，有這樣一群人站了出來——只是手機端可不夠！他們的理想，是讓BERT跑在物聯網裝置上，跑在低功耗晶片上，跑在我們能觸及的每一個電子器件上！

這樣一群來自哈佛/塔夫茨/HuggingFace/康奈爾的軟體和硬體極客們，此刻已披上了法袍，化身為為BERT極限瘦身的煉金術士，向著這個看似不可能的目標新增著許多讓人意想不到的配方…

論文題目：

EdgeBERT: Optimizing On-Chip Inference for Multi-Task NLP

論文連結：

https://arxiv.org/pdf/2011.14203.pdf

Arxiv訪問慢的小夥伴也可以在【夕小瑤的賣萌屋】訂閱號後臺回覆關鍵詞【0105】下載論文PDF~

配方基底：ALBERT

出處：ALBERT: A Lite BERT for Self-supervised Learning of Language Representations（ICLR'20）

連結：https://arxiv.org/pdf/1909.11942.pdf

EdgeBERT是在ALBERT的基礎上進行優化的。

ICLR'20上谷歌提出的ALBERT是目前最佳的BERT壓縮方案。相比於過去利用知識蒸餾從原始BERT模型得到壓縮模型（例如DistilBERT [1]、TinyBERT [2]）和利用浮點數量化得到壓縮模型（例如Q8BERT [3]），ALBERT選擇直接拋棄BERT的預訓練引數，只繼承BERT的設計思想。正所謂不破不立，繼承BERT靈魂的ALBERT僅用12M引數就取得了和其他BERT變體相當的效能。

ALBERT對BERT的設計採取了以下三點改進：

嵌入層分解：BERT中，WordPiece的嵌入維度和網路中隱藏層維度一致。作者提出，嵌入層編碼的是上下文無關資訊，而隱藏層則在此基礎上增加了上下文資訊，所以理應具有更高的維數；同時，若嵌入層和隱藏層維度一致，則在增大隱藏層維數時會同時大幅增加嵌入層引數量。ALBERT因此將嵌入層進行矩陣分解，引入一個額外的嵌入層 $E$ 。設WordPiece詞彙表規模為 $V$ ，嵌入層維度為 $E$ ，隱藏層維度為 $H$ ，則嵌入層引數量可由 $O(V\times H)$ 降低為 $O(V\times E+E\times H)$ 。
引數共享：BERT中，每個Transformer層引數均不同。作者提出將Transformer層的所有引數進行層間共享，從而將引數量壓縮為僅有一層Transformer的量級。
上下句預測任務→句序預測任務：BERT中，除語言模型的MLM任務外還進行了上下句預測任務，判斷句2是否為句1的下一句，然而該任務被RoBERTa和XLNET等模型證實效果一般。作者提出將其替換為句序預測任務，判斷句2和句1之間的句子順序來學習文字一致性。

ALBERT的設計相當成功，成為了壓縮BERT的經典範例，而為了做到最極限壓縮BERT，以ALBERT作為起點確實是個不錯的主意。ALBERT已經如此強大，EdgeBERT又能壓到什麼程度？作者一上來就用一張在QQP上的記憶體佔用/運算量/效能比較圖吊足了讀者的胃口。（注意：縱座標的記憶體佔用量是對數刻度！）

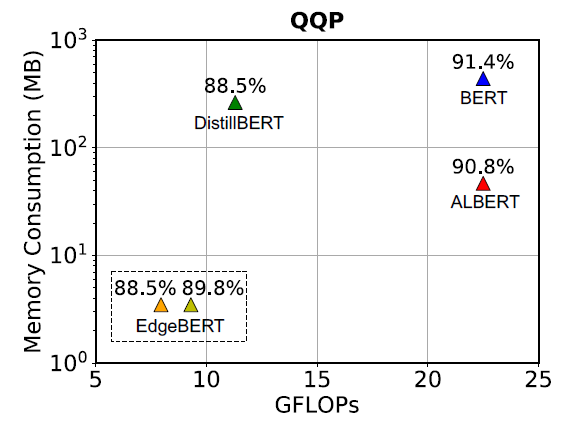
本文對於ALBERT的利用除了作為初始化引數外，還在對下游任務做fine-tune時利用已經fine-tune好的ALBERT作為teacher進行知識蒸餾，來進一步提升模型效能。

初級配方：演算法優化

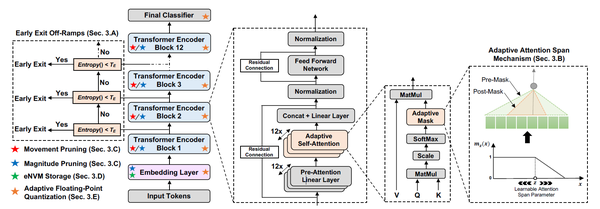
1. 基於熵的提前退出機制

出處：DeeBERT: Dynamic Early Exiting for Accelerating BERT Inference（ACL'20）

連結：https://arxiv.org/pdf/2004.12993.pdf

ALBERT雖好，但Transformer太深了，算起來太慢，讓他變淺一點怎麼樣？

ACL'20的DeeBERT恰好就提出了一種動態的提前退出機制（Early Exit）。這一機制的設計是希望讓簡單的文字經過較少的運算，而複雜的文字經過更多的運算。

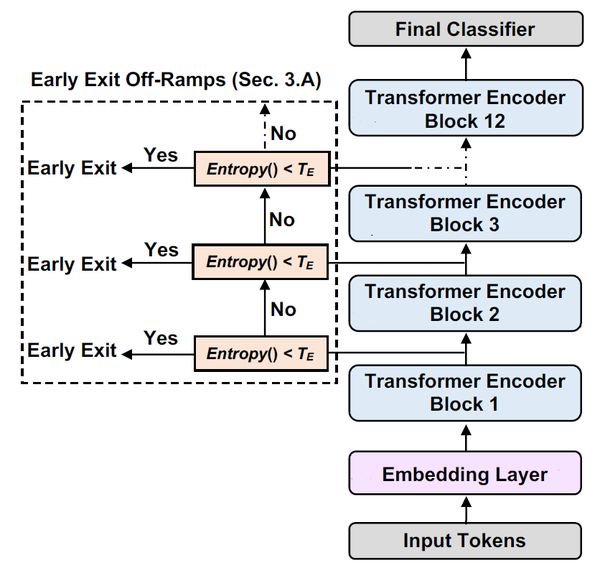
實現上，DeeBERT向 $n$ 層的BERT模型添加了 $(n-1)$ 個“出口層”分類器（Early Exit Off-Ramps）。出口層分類器 $f_i$ 被放置在第 $i$ 和 $i+1$ 層Transformer之間，作為判斷第i層Transformer的資訊是否足以進行推斷的標誌。進行推斷時，從最底層的分類器開始逐層計算出口層分類器的熵，當某一層的出口層分類器熵小於某個閾值時，則將該出口層分類器結果作為模型結果，省去後續層的計算。

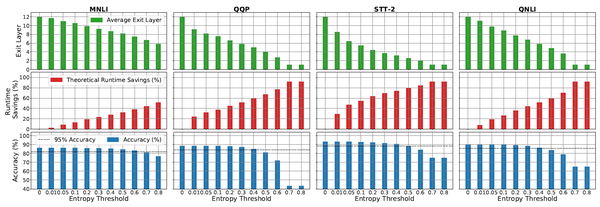
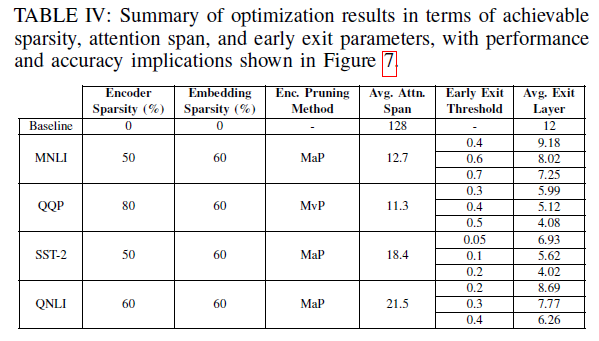
上圖表現的是不同的熵閾值在MNLI、QQP、SST-2、QNLI四個資料集上的平均退出層數、理論執行時間節省和相應的準確度。新增提前退出機制後，在Acc損失1個百分點時，能夠在這四個資料集上分別降低30%、45%、54%和36%的理論執行時間；在Acc損失5個百分點時，能將在這四個資料集上的理論執行時間的降低進一步降低至44%、62%、78%和53%。

2. 動態注意力範圍

出處：Adaptive Attention Span in Transformers（ACL'19）

連結：https://arxiv.org/pdf/1905.07799.pdf

ALBERT雖好，但Attention範圍太廣了，算起來太慢，讓他變窄一點怎麼樣？

ACL'19的Adaptive Attention提出的動態注意力範圍正是試圖通過這種方法減少注意力計算的。在Transformer的多頭自注意力機制中，不同head對應的注意力範圍並不一致，而讓每一個head都對所有token進行注意力運算無疑增添了無用開銷。為此，Adaptive Attention為每一個head新增一個不同的mask，使得每個token只能對周邊的token計算注意力，從而降低矩陣運算的開銷。

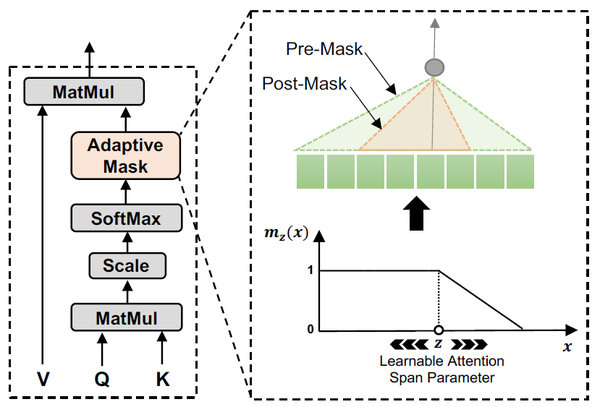
具體地，mask函式 $m_z(x)=\min[\max[\frac{1}{R}(R+z-x)],1]$ 基於兩個token之間的距離為注意力機制的權重計算添加了soft masking。注意力機制中的權重 $\alpha$ 變為：

$\alpha_{tr}=\frac{m_z(t-r)\exp(s_{tr})}{\sum^{t-1}{q=t-S}m_z(t-q)\exp(s{tq})}$

其中 $R$ 為控制soft程度的超引數， $S$ 為序列截止到token $t$ 的長度（原文采用了Transformer Decoder結構學習語言模型，故每個token只能於自己之前的token計算注意力。在EdgeBERT中沒有提及公式，不過根據模型圖的結構來看，分母應修改為對整個序列求和）。mask函式中的 $z$ 為mask的邊界，此邊界值會跟隨注意力的head相關引數和當前輸入序列變化：對於注意力機制中的每一個head $h$ ，有 $z_t=S\sigma(\textbf{v}^T_h\textbf{x}_t+b_h)$ ，其中 $\textbf{v}_h$ 、 $b_h$ 可訓練， $\sigma(\cdot)$ 為sigmoid函式。

EdgeBERT甚至對Adaptive Attention又進一步做了簡化： $z$ 連算都不用算了，直接給每一個head賦一個可學習的 $z_h$ ，連輸入序列都不考慮了，多出來的引數只有12個 $z_h$ （因為有12個head）。那麼，這樣做的結果如何呢？作者將所有序列都pad/trunc到128長度，經過實驗，得到了一個驚人的結果：

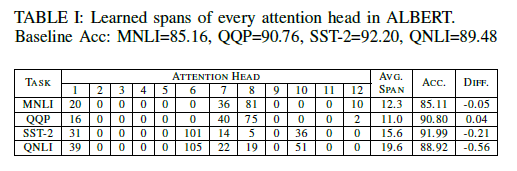
表中展示的是經過優化後各個head的 $z$ 值，和模型在MNLI/QQP/SST-2/QNLI四個任務上的準確度。在一大半head幾乎完全被mask掉（ $z=0$ ）之後，模型居然只在這幾個任務上掉了0.5甚至0.05的準確度！而這一方法也為模型帶來了最高 $1.22\times$ 的計算量降低。

3. 一階網路剪枝

出處：Movement Pruning: Adaptive Sparsity by Fine-Tuning（NeurIPS'20）

連結：https://arxiv.org/pdf/2005.07683.pdf

ALBERT雖好，但引數存起來佔用的記憶體太長了，開銷太大，讓他變短一點怎麼樣？

這裡的網路剪枝方式使用到了NeurIPS'20的一篇針對模型Fine-tune過程的剪枝演算法。該論文的作者提出，傳統的零階網路剪枝（即給模型裡的引數絕對值設定一個閾值，高於它的保留，低於它的置零）的方法並不適用於遷移學習場景，因為該場景下模型引數主要受原始模型影響，卻需要在目標任務上進行fine-tune和測試，所以直接根據模型引數本身剪枝可能會損失源任務或目標任務的知識。與此相反，作者提出一種基於Fine-tune過程中的一階導數進行剪枝的Movement Pruning：儘可能保留fine-tune過程中更加偏離0的引數。

具體地：對於模型引數 $\textbf{W}$ ，為其賦予同樣size的重要性分數 $\textbf{S}$ ，則剪枝mask $\textbf{M}=top_v(\textbf{S})$ 。

前向傳播過程中，神經網路利用加mask的引數計算輸出的各分量 $a_i$ ：

$a_i=\sum^n_{k=1}W_{i,k}M_{i,k}x_k$ 。

反向傳播過程中，利用Straight-Through Estimator[4]的思想，將 $top_v(\cdot)$ 省略近似得到損失函式 $\mathcal{L}$ 對重要性分數 $S$ 的梯度：

$\frac{\partial\mathcal{L}}{\partial S_{i,j}}=\frac{\partial\mathcal{L}}{\partial a_i}\frac{\partial a_i}{\partial S_{i,j}}=\frac{\partial \mathcal{L}}{\partial a_i}W_{i,j}x_j$

對模型引數，有：

$\frac{\partial\mathcal{L}}{\partial W_{i,j}}=\frac{\partial \mathcal{L}}{\partial a_i}M_{i,j}x_j$

將上述兩個式子代換後，省略 ${0,1}$ 的mask矩陣 $M_{i,j}$ 後可得：

$\frac{\partial\mathcal{L}}{\partial S_{i,j}}=\frac{\partial \mathcal{L}}{\partial W_{i,j}}W_{i,j}$

根據梯度下降，當 $\frac{\partial \mathcal{L}}{\partial S_{i,j}}<0$ 時，重要性 $S_{i,j}$ 增大，此時 $\frac{\partial \mathcal{L}}{\partial W_{i,j}}$ 與 $W_{i,j}$ 異號。這表示，只有當在反向傳播時為正的引數變得更大或為負的引數變得更小時才會得到更大的重要性分數，避免被剪枝。

4. 零階網路剪枝

出處：Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding（ICLR'16）

連結：https://arxiv.org/pdf/1510.00149.pdf

變短是變短了，但感覺這剪得還不夠好啊，再換一種演算法讓它更短一點怎麼樣？

這種方法的做法非常簡單：給模型裡的引數設定一個絕對值閾值，絕對值高於它的保留，絕對值低於它的置零。由於方法實在太過簡單，不用公式也能很容易理解的吧(=・ω・=)

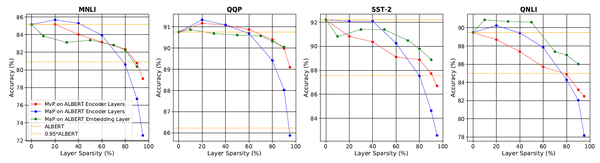
一階和零階網路剪枝的效果對比如上圖所示（MvP：一階網路剪枝，MaP：零階網路剪枝）。在引數稀疏程度更高時，一階剪枝的效果更好，其他情況下是簡單的零階剪枝更有效。同時，研究還發現，當剪掉95%的嵌入層引數時，模型竟然在4個任務上都保持了至少95%的準確度。

5.動態浮點數量化

出處：AdaptivFloat: A Floating-point based Data Type for Resilient Deep Learning Inference（arXiv Preprint）

連結：https://arxiv.org/pdf/1909.13271.pdf

誒，怎麼還有？網路的運算和儲存過程從深度、寬度和長度進行了全方位的優化，模型還能再輕？

的確，到此為止，一般的煉丹師已經看著自己三維裁剪過的模型感到成就感滿滿了，但這距離讓BERT跑遍所有裝置的目標還差得遠。以下的部分就要開始深入一般NLP工程師見不到的第四個維度——硬體維度了。在深入硬體優化之前，先來道偏軟體的開胃菜，看看如何在浮點數量化上下手優化儲存吧！

我們平時在考慮利用浮點數特性進行計算加速時，最先考慮的是使用FP16混合精度，雖然有效，但畢竟損失了資訊，效果也多多少少會受影響。既想保留精度又想加速訓練減小儲存，那就只有深入底層，修改浮點數的表示方法了！

這正是AdaptivFloat的初衷：設計一種更加適合深度學習場景的浮點數資料型別。不過，要講明白AdaptivFloat資料型別需要涉及到一些與機器學習無關的知識。

根據IEEE 754二進位制浮點數標準，一個浮點數的二進位制表示由三個域組成：符號位（Sign，S）、指數偏移值（Exponent bias，E）和分數值（Fraction，或Mantissa，F）。由此，一個數可以表示為 $V=S\times2^{E_{real}}\times F$ 。

這時聰明的你可能發現有什麼不對勁：按照表示無符號整形的方法取指數偏移值只能取出正數啊！2的負次冪怎麼辦！這正是為什麼稱其為“指數偏移值”：它並不代表實際上2的指數，而是在其基礎上需要加一個常數作為2的指數： $E_{real}=E+E_{bias}$ 。

我們常用的浮點數保證了 $E_{bias}$ 的選取能夠使得 $E_{real}$ 在數軸兩側分佈幾乎均等（例如在32位浮點數FP32中，指數範圍為-126至+127），但這樣的數作為機器學習模型的引數顯然有些不太合適：為了增加小數的精度，我們甚至要允許 $2^{127}$ 這樣顯然不會出現的數也能表示，這真的不是在浪費記憶體？

AdaptivFloat的最關鍵動機正在於此：根據模型引數動態修改 $E_{bias}$ 。所謂動態體現在每個Tensor都能得到量身定做的 $E_{bias}$ 。方法也很簡單，找到Tensor裡最大的一個數，讓它能被指數範圍恰好覆蓋到就好。不過說來簡單，為了實現這一方法需要配套地對現有浮點數表示方法進行許多其他修改，感興趣的話可以去看看AdaptivFloat原文，此外IEEE 754標準[5]同樣也可以作為參考哦~

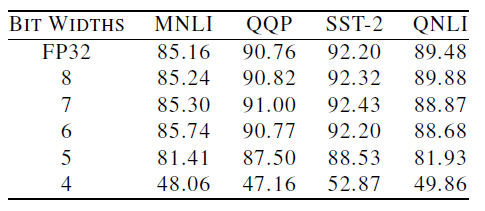
上圖的結果中，Bit Width是浮點數的總位數，後五行在模型中使用了AdaptivFloat並將指數偏移值限制為3個bit。不比不知道，誰能想到修改個量化方式居然直接用8bit在四個資料集上都幹翻了FP32？！不僅節省了3/4的記憶體，還取得了更好的效能，或許這就是吹毛求疵挑戰極限的極客們的浪漫？

高階配方：儲存介質選擇

光軟體優化可不夠！如果軟體優化就夠了的話，還買什麼SSD，換什麼GPU（不）

EdgeBERT的目的，是儘可能降低邊緣計算場景中使用BERT的推理延遲和耗能。為了最大限度地降低推理延遲，需要為網路中不同的組成部分根據其增刪改查的需求選取符合最大效能的儲存介質。

BERT類模型的一大特點，在於它們都是預訓練模型：這類模型並非開箱即用，而是需要在目標任務上fine-tune後才能使用。這使得這類模型天生地存在著兩類儲存需求：

嵌入層：儲存了Embedding向量。EdgeBERT在進行下游任務fine-tune時一般不對嵌入層進行修改。這類引數相當於只讀引數，只對快速讀取有較高要求，同時希望能夠在掉電時依然保持原有資料來降低資料讀寫開銷，因此適用耗能低、讀取速度快的eNVM（Embedded Non-Volatile Memory，嵌入式非揮發性記憶體）。本文選取的是基於MLC的ReRAM，一種低功耗、高速度的RAM。
其他引數：這些引數需要在fine-tune時進行改變。此處使用的是SRAM（與計算機記憶體的DRAM不同，SRAM更貴但功耗更低、頻寬更高，常被用於製造cache或暫存器）

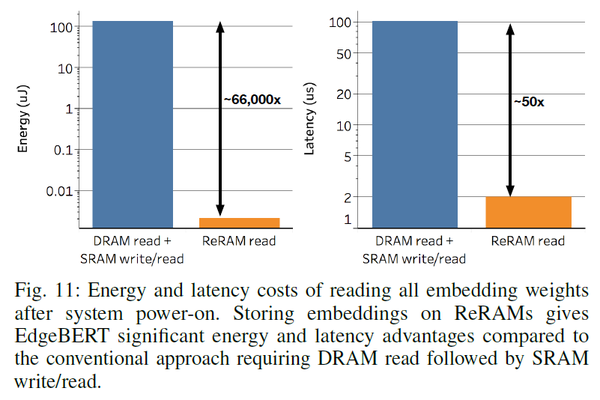
嵌入層用了ReRAM究竟能帶來多大的影響？上圖結果表明，僅僅是改變了嵌入層的硬體介質就能帶來約 $50\times$ 的推理延遲降低，以及低至約 $66000\times$ 的能耗降低！這對於邊緣計算場景下簡直是質變了！（為何ReRAM只有讀，但DRAM那邊卻要算DRAM讀+SRAM讀/寫呢？因為此處的ReRAM是特殊設計的只讀結構，並且可以直接讀入處理器進行運算。與此相反，DRAM，即電腦裡一般使用的記憶體，需要經過基於SRAM的處理器cache，所以讀寫開銷需要加上這部分讀寫開銷。）

合併結果

好了，所有的基礎配方一個一個單獨使用的結果已經出來了！那麼，把它們全都加在一起能產生什麼樣的結果呢？

這張圖展示了完全體EdgeBERT在四個資料集上的效能、運算量和記憶體佔用。其中所有紅點的實驗配置參照上表（即TABLE IV）。

在效能（準確度）相比ALBERT下降1個百分點時，EdgeBERT能取得 $13.4\times$ 的記憶體降低和 $2.4\times$ 的推理速度；下降5個百分點時甚至能取得 $3.53\times$ 的推理速度。
Embedding經過裁剪後僅保留了40%，使得儲存進eNVM的嵌入層引數僅1.73MB。
QQP的Transformer引數被mask掉80%，MNLI、SST-2、QNLI的Transformer引數被mask掉60%後，效能可以僅下降1個百分點。

究極配方：硬體加速器

這是什麼東西？來，給你展示一下谷歌給樹莓派定製的TPU加速器Coral：

EdgeBERT專屬的硬體加速器想來應該也是差不多的樣子。

這一部分完全不是王蘇的菜…給各位上一張EdgeBERT加速器的硬體結構圖：

感興趣的各位可以去參照原文進行學習_(:з」∠)_

這個加速器有什麼用呢？它是基於EdgeBERT的運算特點量身定做的加速器，能夠把fine-tune好的EdgeBERT完整地裝進去進行運算。至於運算效果，它們修改了模型圖中VMAC序列（即進行矩陣運算的單元序列）長度，與NVIDIA的移動端TX2 mGPU進行了推理時間和耗能的對比：

本文中提出的硬體加速器能夠為EdgeBERT帶來相比於baseline硬體加速器 $5.2\times$ 的能耗降低，相比於英偉達TX2移動端GPU甚至能夠帶來 $163\times$ 的能耗降低！耗電大戶BERT家族終於也有能被說“省電”的一天了！

總結

壓縮BERT是一項研究，但極限壓縮BERT則是一項不易完成的工程：無論是對Transformer模型的全方位裁剪，還是對硬體儲存介質讀寫效能與容錯的取捨，亦或是對專屬硬體加速器的設計，單獨拿出一項已足夠艱難，將它們合在一起就不僅可能互相沖突，甚至還可能產生逆向優化。這篇文章通過大量的實驗，測試了已有的幾種優化方法在邊緣計算場景下的效能，比較了不同優化方法之間的差別，分析了所有優化方法進行組合後的影響及效果，並進一步提出了專屬的硬體結構，實現了對目前已有的最輕量BERT變體的即插即用。對於需要長待機、低功耗、短延遲的場景，例如智慧家居或是其他需要NLP技術加持的物聯網裝置，或許我們真的能在不遠的將來看到實體的類似EdgeBERT加速器的解決方案出現。

雖然我們對於可能帶來更大變革的模型結構依然處在探索當中，但從當下實用的角度而言，用基於Lottery Ticket Hypothesis[6]的BERT優化方法尋找一個更優的類BERT子結構依然是一個不錯的課題，至少它能讓更多人、更多時候、更多場景能夠用上效能強大的預訓練模型。本文中提到的這些優化方法是不是也給愛思考的你帶來了什麼啟發呢？

參考文獻

[1] Sanh et al. DistilBERT, a Distilled Version of Bert: Smaller, Faster, Cheaper and Lighter. In NeurIPS'19 EMC2 Workshop. https://arxiv.org/pdf/1910.01108.pdf [2] Jiao et al. TinyBERT: Distilling BERT for Natural Language Understanding. In Findings of EMNLP'20. https://arxiv.org/pdf/1909.10351.pdf [3] Zafrir et al. Q8BERT: Quantized 8Bit BERT. In NeurIPS'19 EMC2 Workshop. https://arxiv.org/pdf/1910.06188.pdf [4] Bengio et al. Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation. arXiv Preprint. https://arxiv.org/pdf/1308.3432.pdf [5] IEEE 754 - Wikipedia. https://zh.wikipedia.org/wiki/IEEE_754 [6] Frankle et al. The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks. In ICLR'19. https://arxiv.org/pdf/1803.03635.pdf

「其他文章」